heureka

A regular hexagon has vertices at $1-i, 0, a, b, c, d$ clockwise in that order, as in the picture below:

Then what is \(\operatorname{Im}(a)\)?

\(\begin{array}{|rcll|} \hline \sin(75^{\circ}) &=& \dfrac{\operatorname{Im}(a)} {\sqrt{2}} \\ \operatorname{Im}(a) &=& \sqrt{2}\cdot \sin(75^{\circ}) \\ \operatorname{Im}(a) &=& 1.41421356237\cdot 0.96592582629 \\ \mathbf{\operatorname{Im}(a)} & \mathbf{=} & \mathbf{1.36602540378} \\ \hline \end{array}\)

Hello Melody,

a happy new year.

Suppose that ABCD is a trapezoid in which AD||BC. 

Given AC is perpendicular to CD, AC bisects angle BAD, 

and the area of ABCD is 42, 

then compute the area of triangle ACD.

\(\text{Let $AB=a$ } \\ \text{Let $\angle BAC = \angle CAD = \alpha$ } \)

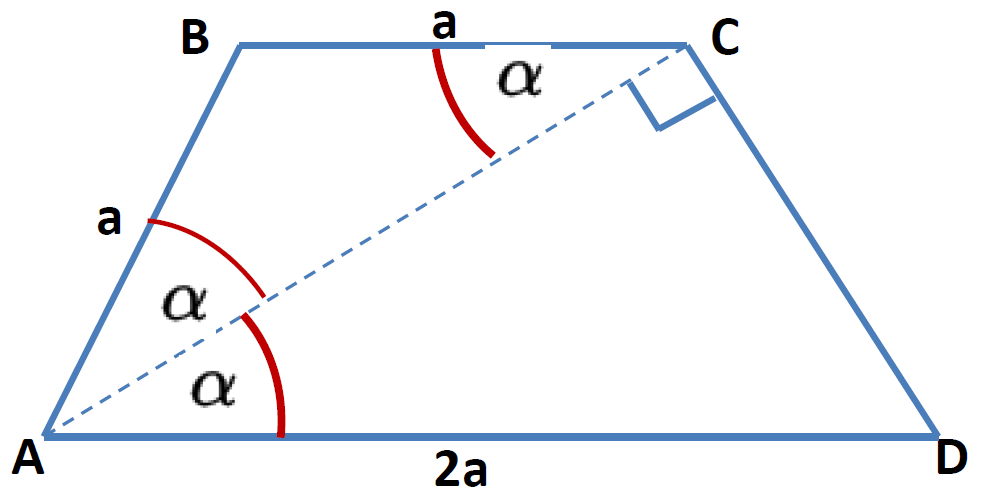
\(\text{Let $\angle ACB = \angle BAC = \alpha \qquad ( AD\parallel BC) $ } \)

sin - rule

\(\begin{array}{|rcll|} \hline \dfrac{ \sin(\angle BAC) } {BC} &=& \dfrac{ \sin(\angle ACB) } {AB} \\ \dfrac{ \sin(\alpha) } {BC} &=& \dfrac{ \sin(\alpha) } {AB} \\ BC &=& AB \quad & | \quad AB=a \\ & \boxed{BC = a} \\ \hline \end{array} \)

\(\text{Let $\angle ABC = 180^{\circ}-2\alpha $}\)

cos - rule

\(\begin{array}{|rcll|} \hline (AC)^2 &=& (BC)^2+(AB)^2-2\cdot BC \cdot AB \cdot \cos(180^{\circ}-2\alpha) \\ (AC)^2 &=& 2a^2+2a^2\cos( 2\alpha) \\ (AC)^2 &=& 2a^2(1+\cos(2\alpha)) \quad | \quad \cos( 2\alpha)=2\cos^2(\alpha)-1 \\ (AC)^2 &=& 2a^2\cdot ( 1+2\cos^2(\alpha)-1 ) \\ (AC)^2 &=& 2a^2\cdot 2\cos^2(\alpha) \\ (AC)^2 &=& 4a^2\cdot \cos^2(\alpha) \\ & & \boxed{ AC= 2a\cos(\alpha)} \quad | \quad \cos( \alpha)= \dfrac{AC}{AD} \\ AC &=& 2a\dfrac{AC}{AD} \\ 1 &=& \dfrac{2a}{AD} \\ & & \boxed{ AD= 2a } \\ \hline \end{array}\)

\(\mathbf{A_{\triangle} = \ ?} \)

\(\begin{array}{|rcll|} \hline A_{ABCD} &=& \left( \dfrac{AD+BC}{2} \right) \cdot h \quad | \quad AD= 2a,\quad BC = a \\ A_{ABCD} &=& \left( \dfrac{2a+a}{2} \right) \cdot h \\ A_{ABCD} &=& \dfrac{3}{2} a \cdot h \quad | \quad A_{ABCD}=42 \\ 42&=& \dfrac{3}{2} a \cdot h \\ a \cdot h &=& \mathbf{ \dfrac{2}{3} \cdot 42 } \\ \mathbf{a \cdot h} &\mathbf{=}& \mathbf{ 28 } \\\\ A_{\triangle} &=& \dfrac{AD\cdot h}{2} \quad | \quad AD= 2a \\ A_{\triangle} &=& \dfrac{2a\cdot h}{2} \\ A_{\triangle} &=& a\cdot h \quad | \quad a\cdot h = 28 \\ \mathbf{A_{\triangle}} &\mathbf{=}& \mathbf{ 28} \\ \hline \end{array}\)

The area of triangle ACD is 28.

Hello Rom,

i switch it to an alternating series, because the question is: 0.1₂  -  0.01₂ + 0.001₂ - 0.0001₂ + 0.00001₂ +- ...

and the answer is a fraction.

\(\begin{array}{|rcll|} \hline r &=& \dfrac{ {\color{red}-}\dfrac{1}{4} } { \dfrac{1}{2} } = {\color{red}-}\dfrac{1}{2} \\\\ r &=& \dfrac{ \dfrac{1}{8} } { {\color{red}-}\dfrac{1}{4} } = {\color{red}-}\dfrac{1}{2} \\ \ldots \\ \hline \end{array}\)

Limits
I was just reviewing my calc book when I stumbled across this problem.
\(\large { \lim \limits_{x \to \infty} \dfrac{\sqrt{x^4-10x}-\sqrt{x^4-5x^2+7}}{5} }\)

\(\begin{array}{|rcll|} \hline &&\mathbf{ \lim \limits_{x \to \infty} \dfrac{\sqrt{x^4-10x}-\sqrt{x^4-5x^2+7}}{5} } \\\\ &=&\dfrac15 \cdot \lim \limits_{x \to \infty} \left( \sqrt{x^4-10x}-\sqrt{x^4-5x^2+7} \right) \\\\ &=&\dfrac15 \cdot \lim \limits_{x \to \infty} \left( \sqrt{x^4-10x}-\sqrt{x^4-5x^2+7} \right) \dfrac{\left( \sqrt{x^4-10x}+\sqrt{x^4-5x^2+7} \right)}{\left( \sqrt{x^4-10x}+\sqrt{x^4-5x^2+7} \right)} \\\\ &=&\dfrac15 \cdot \lim \limits_{x \to \infty} \left( \dfrac{ x^4-10x-(x^4-5x^2+7)} { \sqrt{x^4-10x}+\sqrt{x^4-5x^2+7} } \right) \\\\ &=&\dfrac15 \cdot \lim \limits_{x \to \infty} \left( \dfrac{ 5x^2-10x-7} { \sqrt{x^4-10x}+\sqrt{x^4-5x^2+7} } \right) \cdot \dfrac{x^2}{x^2} \\\\ &=&\dfrac15 \cdot \lim \limits_{x \to \infty} \left( \dfrac{ \frac{5x^2-10x-7} {x^2} } { \frac{\sqrt{x^4-10x}+\sqrt{x^4-5x^2+7}} {x^2} } \right) \\\\ &=&\dfrac15 \cdot \lim \limits_{x \to \infty} \left( \dfrac{ \frac{5x^2-10x-7} {x^2} } { \sqrt{\frac{x^4-10x} {x^4} }+\sqrt{ \frac{x^4-5x^2+7} {x^4} } } \right) \\\\ &=&\dfrac15 \cdot \lim \limits_{x \to \infty} \left( \dfrac{ 5-\frac{10}{x}-\frac{7}{x^2} } { \sqrt{1-\frac{10}{x^3} } + \sqrt{1-\frac{5}{x^2}+\frac{7}{x^4}} } \right) \\\\ &=&\dfrac15 \cdot \left( \dfrac{ 5-0-0 } { \sqrt{1-0 } + \sqrt{1-0+0} } \right) \\\\ &=&\dfrac15 \cdot \left( \dfrac{ 5 } { 1 + 1 } \right) \\\\ &=&\dfrac15 \cdot \dfrac{ 5 } {2 } \\\\ &\mathbf{=}&\mathbf{\dfrac12} \\ \hline \end{array}\)

In the figure, angle A = 28 degrees, angle B = 74 degrees and angle C = 26 degrees. 

If x and  y are the measures of the angles in which they are shown, what is the value of x+y?

\(\begin{array}{|rcll|} \hline x-A-B+y &=& C \\ x+y &=& A+B+C \\ x+y &=& 28^{\circ} + 74^{\circ} + 26^{\circ} \\ \mathbf{x+y} & \mathbf{=} & \mathbf{128^{\circ}} \\ \hline \end{array}\)

Find the sum of the base-2 geometric series
\(0.1_2-0.01_2+0.001_2-0.0001_2+0.00001_2\ldots\);
give your answer as a fraction in which the numerator and denominator are both expressed in base 10.

\(\begin{array}{|rcll|} \hline 0.1_{2} = 1\cdot 2^{-1} &=& \frac{1}{2} \\ 0.01_{2} = 1\cdot 2^{-2} &=& \frac{1}{4} \\ 0.001_{2} = 1\cdot 2^{-3} &=& \frac{1}{8} \\ 0.0001_{2} = 1\cdot 2^{-4} &=& \frac{1}{16} \\ 0.00001_{2} = 1\cdot 2^{-5} &=& \frac{1}{32} \\ \ldots \\ \hline \end{array}\)

Infinite Geometric Series:

\(\begin{array}{|rcll|} \hline s &=& \dfrac{1}{2} - \dfrac{1}{4} + \dfrac{1}{8} - \dfrac{1}{16} + \dfrac{1}{32} \pm \ldots \quad | \quad a=\frac{1}{2},~ r = -\frac{1}{2} \\\\ s &=& \dfrac{a}{1-r} \quad | \quad |r| < 1. \\\\ s &=& \dfrac{\frac{1}{2}}{1- \left(-\frac{1}{2} \right)} \\\\ s &=& \dfrac{\frac{1}{2}}{1+\frac{1}{2}} \\\\ s &=& \dfrac{\frac{1}{2}}{\frac{3}{2}} \\\\ s &=& \dfrac{1}{2} \cdot \dfrac{2}{3} \\\\ \mathbf{s} & \mathbf{=} & \mathbf{\dfrac{1}{3}} \\ \hline \end{array} \)

What is the smallest integer n, greater than 1, such that
\(n^{-1} \pmod{130}\)
and
\(n^{-1} \pmod{231} \)
are both defined?

\(\text{$n$ must be coprime to $130$ and $231$ } \\ \text{respectively $\gcd(n,130) = \gcd(n,231) = 1$ }\)

Factorisation:

\(\begin{array}{|rcll|} \hline 130 &=& 2\times 5 \times 13 \\ 231 &=& 3\times 7 \times 11 \\ \hline \end{array}\)

\(\text{The next prime number after $2,3,5,7,11,13$ is ${\color{red}17}$ }\)

So 17 is the smallest integer, greater than 1.

\(17^{-1} \pmod {130} = 23 \\ 17^{-1} \pmod {231} = 68 \)

Hello Melody,

of course there is x = 8.

c.)

hab ich ja gesagt dass der Pfeil etwas schräg ist hier ein Bild damit es etwas deutlicher wird.

Ändert sich das Ergebnis der Aufgabe bezüglich des Pfeiles ?

\(\displaystyle \lim \limits_{x\searrow 0} \dfrac{\ln\Big(\cos(x) \Big)} {\ln\Big(\cos(3x)\Big) } \qquad \text{von rechts annähern}\)

\(\begin{array}{|rcll|} \hline x &=& 0+\dfrac{1}{n} \\ &=& \dfrac{1}{n} \\ \hline \end{array}\)

\(\displaystyle \lim \limits_{n\to \infty} \dfrac{\ln\Big(\cos(\frac{1}{n}) \Big)} {\ln\Big(\cos(\frac{3}{n})\Big) }\)

Bernoulli / de l'Hospital

\(\begin{array}{|rcl|} \hline && \mathbf{\lim \limits_{n\to \infty} \dfrac{\ln\Big(\cos(\frac{1}{n}) \Big)} {\ln\Big(\cos(\frac{3}{n})\Big) } } \quad | \quad \text{Bernoulli / de l'Hospital } \\\\ &=& \lim \limits_{n\to \infty} \dfrac{\dfrac{-\sin(\frac{1}{n})}{\cos(\frac{1}{n})}} {\dfrac{-3\sin(\frac{3}{n})}{\cos(\frac{3}{n})} } \\\\ &=& \lim \limits_{n\to \infty} \dfrac{1}{3}\cdot \dfrac{\sin(\frac{1}{n})\cos(\frac{3}{n})} {\cos(\frac{1}{n})\sin(\frac{3}{n})} \\\\ && \begin{array}{|rcl|} \hline \sin(\frac{1}{n})\cos(\frac{3}{n}) &=& \dfrac12\cdot \Big( \sin(\frac{1}{n}-3\cdot \frac{1}{n})+ \sin(\frac{1}{n}+3\cdot \frac{1}{n}) \Big) \\ &=& \dfrac12\cdot \Big( \sin(-2\cdot \frac{1}{n})+ \sin(4\cdot \frac{1}{n}) \Big) \\ &=& \dfrac12\cdot \Big( \sin(4\cdot \frac{1}{n})-\sin(2\cdot \frac{1}{n}) \Big) \\ &=& \dfrac12\cdot \Big( 2\sin(2\cdot \frac{1}{n})\cos(2\cdot \frac{1}{n})-\sin(2\cdot \frac{1}{n}) \Big) \\ &=& \dfrac12\cdot\sin(2\cdot \frac{1}{n}) \Big( 2\cos(2\cdot \frac{1}{n})-1 \Big) \\ \hline \end{array}\\ && \begin{array}{|rcl|} \hline \sin(\frac{3}{n})\cos(\frac{1}{n}) &=& \dfrac12\cdot \Big( \sin(3\cdot \frac{1}{n}-\frac{1}{n})+ \sin(3\cdot \frac{1}{n}+\frac{1}{n}) \Big) \\ &=& \dfrac12\cdot \Big( \sin(2\cdot \frac{1}{n})+ \sin(4\cdot \frac{1}{n}) \Big) \\ &=& \dfrac12\cdot \Big( \sin(4\cdot \frac{1}{n})+\sin(2\cdot \frac{1}{n}) \Big) \\ &=& \dfrac12\cdot \Big( 2\sin(2\cdot \frac{1}{n})\cos(2\cdot \frac{1}{n})+\sin(2\cdot \frac{1}{n}) \Big) \\ &=& \dfrac12\cdot\sin(2\cdot \frac{1}{n}) \Big( 2\cos(2\cdot \frac{1}{n})+1 \Big) \\ \hline \end{array}\\\\ &=& \lim \limits_{n\to \infty} \dfrac{1}{3}\cdot \dfrac{\dfrac12\cdot\sin(2\cdot \frac{1}{n}) \Big( 2\cos(2\cdot \frac{1}{n})-1 \Big)} {\dfrac12\cdot\sin(2\cdot \frac{1}{n}) \Big( 2\cos(2\cdot \frac{1}{n})+1 \Big)} \\\\ &=& \lim \limits_{n\to \infty} \dfrac{1}{3}\cdot \dfrac{\Big( 2\cos(2\cdot \frac{1}{n})-1 \Big)} {\Big( 2\cos(2\cdot \frac{1}{n})+1 \Big)} \quad |\quad \lim \limits_{n\to \infty} \frac{1}{n} = 0 \\\\ &=& \dfrac{1}{3}\cdot \dfrac{\Big( 2\cos(0)-1 \Big)} {\Big( 2\cos(0)+1 \Big)} \quad | \quad \cos(0)=1 \\\\ &=& \dfrac{1}{3}\cdot \dfrac{\Big( 2\cdot 1-1 \Big)} {\Big( 2\cdot 1+1 \Big)} \\\\ &=& \dfrac{1}{3}\cdot \dfrac{ 1 } { 3 } \\\\ &\mathbf{=}& \mathbf{ \dfrac{1}{9} } \\ \hline \end{array} \)