CPhill

3x - 4y  = 5

x axis intersection , let y = 0

3x = 5

x = 5/3

y axis intersection, let x =0

-4y = 5

y = -5/4

AB  = sqrt  [ (5/3)^2  + (-5/4)^2 ] =   sqrt [ 25/9 + 25/ 16 ]  = [ sqrt [ (9 + 16)(25) / (16 * 9) ] = 

sqrt [ 25^2 / 144]  =   25 / 12

Originally we have that :

(2/5)X =Y      (1)

After he sells 44 marvles from bag X, we have this situation :

(5/7) (X -44) = Y      (2)  

Sub (2)  into (1)

(5/7)(X -44)  =(2/5)X

(5/7)X  - 220/7 = (2/5)X

[ 5/7 - 2/5 ] X  =  220/7

[ 11/35]X = 220/7

X = 220/7 * 35/11  =100 marbles originally in X

Check  

Otiginally

X =100

Y = (2/5) 100 =  40

After he sells 44 marbles from X  we have that

X = (5/7)(100 - 44)  = (5/7) (56) = 40  =  the number in Y = (2/5)*100

Translate the top circle  with the equation  x^2 + (y-2)^2  = 16   to the bottom circle

 with the equation x^2 + y^2 = 16

Let Area A be the area of rhombus ACBD =  4^2 * sin (151.04°) ≈ 7.75

Let Area A  + Area B  = the area of the portion of the bottom circle bounded by minor arc  CED  = 

pi * 4^2 * (151.04 / 360) ≈ 21.09

Area B  = Area A + Area B - Area A  21.09 - 7.75 ≈ 13.35

Let Area B + Area C  = the area of the portion of the top circle bounded by major arc CFD = 

pi * 4^2 * ( 360 -151.04) / 360 ≈ 29.18

The area swept out by the translation of the top circle to the bottom circle  = 

Area  B + Area  C - Area B  =   Area C   = 29.18 - 13.35  ≈ 15.84

We can  divide the octagon into 8 congruent triangles

AB = the base of each = 1

Height = h   of each triangle  can be found as

(1/2) / sin (22.5°)  =  h / sin (67.5 °)

(1/2) / sin (22.5°) = h / cos (22.5°)

h = (1/2) cos (22.5°) / sin (22.5°)   

h = (1/2) cot (22.5°) ≈ 1.207

Area =  8 (1/2) (1) (1.207)  ≈  4.828

Call the total sold =T

A = (1/5)T

C = (1/5)T + 12

G = (1/5) T

J = 30

(1/5)T + (1/5)T + 12 + (1/5)T + 30  =  T            simplify

(3/5)T + 42  = T

42 = T - (3/5)T

42 = (2/5)T

T  = 42 ( 5/2)  =  105

A + B +C  = 60

(7/10)A  = B +(3/10)A   →   B = (4/10)A

(4/5)A = C + (1/5)A  → C = (3/5)A

So

A + (4/10)A +(3/5)A = 60

A +A = 60

2A =60

A =30

B = (4/10) (30)  = 12

C = (3/5)(30) = 18

a) C had   18  -12  =  6 more marbles than B at the start 

b) B had  12/60  = 1/5 of the total at first

Call the total number of  cupcakes =T

2/9  T of the original batch were chocolate and 7/9 T of the original batch were strawberry

After selling (1/2) of the strawberry cupcakes he had  (7/9)T * (1/2)  = (7/18) T left

And  that number was 285 more than the number of chocolate xupcakes

So

(7/18) T - 285 = (2/9)T

(7/18) - 285  = (4/18) T

(7/18 - 4/18) T = 285

( 3/18) T = 285

(1/6) T =286

T = 285 * 6 /1 =  1710 cupcakes were baked

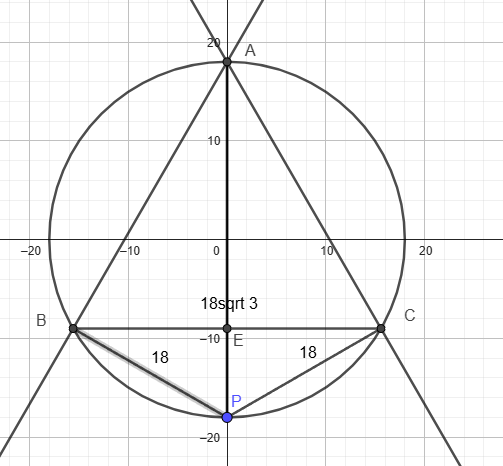
ABPC is a quadrilateral  inscribed in the circle

Angle BAC  = 60°

So angle BPC is supplemental to angle BAC  = 120°

Using the Law of Cosines

BC^2 = PB^2 + PC^2  - 2(PB *  PC) cos (120°)

BC^2 = 18^2 + 18^2 - 2(18*18( (-1/2)

BC^2 = 18^2 + 18^2 + 18^2

BC^2 = 3*18^2

BC = 18sqrt (3) = side of the equilateral triangle

Triangle AEC is a 30-60-90 right triangle

AC = 18sqrt (3) = the hypotenuse

AE is opposite the 60° angle =  18sqrt 3 * (sqrt 3 /2)  =  27

Triangle PEC is also a 30-60-90 right triangle

EC = 9sqrt 3  is opposite the 60° angle

PE is opposite the 30° angle  = 9sqrt 3/sqrt 3 = 9

PA = PE + AE =  9 + 27 =  36

Slope between A and C =  (8 -4) / (6 -3) = 2/3

So D =  (4 + 3 , -1 + 2) =  (7, 1)

I oriented the spheres  like  this

We can set up similar  triangles AEC and BDC

We have that

AE/ AC = BD / BC

FC = x

AE= 4

AC = 6 + x

BD = 1

BC = 1 + x

So

4/ (6 +x) = 1/ (1 + x)

4(1 + x) = 6 +x

4 + 4x = 6 + x

3x = 2

x = 2/3

C = ( 4 + 2 + 2/3 , 0)  =  (20/3 , 0)

HC  = 6+ 2 + x  =   6 + 2 + 2/3  =  26/3  = height of cone

We can find DC  as  sqrt  ( (5/3)^2 -1 )  =sqrt ( 25/9 - 9/9) = sqrt (16/9) =  4/3

The equation of the tangent line to both circles through D  has the slope = -BD/DC =  -1/ ( 4/3) = -3/4

And the equation of this line  is

y = (-3/4)(x -20/3)

The intersection of this  line with the line x =- 4  gives us the radius of the cone =

y = (-3/4)(-4 -20/3)  = (-3/4)(-32/3) =  8 = GH

So the volume of the cone =  (1/3)pi  GH^2 * HC =  (1/3)pi * 8^2 * (26/3)  = (1664/9) pi