hectictar

\(\dfrac{10!+11!+12!}{10!+11!}\\~\\ \ =\ \dfrac{10!\ +\ 11\cdot10!\ +\ 12\cdot11\cdot10!}{10!\ +\ 11\cdot10!}\\~\\ \ =\ \dfrac{10!(\ 1\ +\ 11\ +\ 12\cdot11\ )}{10!(\ 1\ +\ 11\ )}\\~\\ \ =\ \dfrac{1\ +\ 11\ +\ 12\cdot11}{1\ +\ 11}\\~\\ \ =\ \dfrac{1\ +\ 11\ +\ 132}{1\ +\ 11}\\~\\ \ =\ \dfrac{144}{12}\\~\\ \ =\ 12\)

_

\(\displaystyle \sqrt{\frac{16}{25}+\frac{9}{4}}\ =\ \sqrt{\frac{16\cdot4}{25\cdot4}+\frac{9\cdot25}{4\cdot25}}\ =\ \sqrt{\frac{64}{100}+\frac{225}{100}}\ =\ \sqrt{\frac{289}{100}}\ =\ \frac{\sqrt{289}}{\sqrt{100}}\ =\ \frac{17}{10}\)

The question is:

\(\frac34\)   times what is  \(6\frac12\)    ?

\(\frac34x\ =\ 6\frac12\)

Divide both sides of the equation by  3/4

\(x\ =\ 6\frac12\div\frac34\\~\\ x\ =\ \frac{13}{2}\div\frac34\\~\\ x\ =\ \frac{13}{2}\times\frac43\\~\\ x\ =\ \frac{13}{1}\times\frac23\\~\\ x\ =\ \frac{13\times2}{1\times3}\\~\\ x\ =\ \frac{26}{3}\\~\\ x\ =\ 8\frac{2}{3}\)

So...

\(\frac34\)   times  \(8\frac23\)  is  \(6\frac12\)    ...in other words:

The number of times that  \(\frac34\)   goes into  \(6\frac12\)   is  \(8\frac23\)

Imagine there are only 4 characters: a, b, c, and  d

And we want to know how many strings of length 3 can be made with those 4 characters.

First let's list all of the strings that start with  'a' :

aaa

aab

aac

aad

aba

abb

abc

abd

aca

acb

acc

acd

ada

adb

adc

add

There are 4 groups of 4 which means there are  4 * 4 = 16 strings in the above list.

Now imagine if we kept the pattern going. We could copy and paste the above list and change all of the first characters in each string to "b". Then we could paste it again and change all of the first letters to "c", and again for "d". That would make 4 total groups: the first group all start with "a", second group all start with "b", the third all start with "c" and the fourth all start with "d".

So then there would be a total of  4 * 4 * 4 = 4³  =  64 strings  in the completed list.

So the total number of strings is  4³  , which is the number of different characters raised to the power of the length of the string.

I hope this helps explain a little bit where the  62⁷  comes from!

the number of unique characters   =   10 + 26 + 26   =   62

the number of unique strings of 7 such characters   =   62⁷   =   3 521 614 606 208

That's over 3 trillion!

x + y  =  10     Subtract  y  from both sides of this equation to get     x  =  10 - y

Now since   x = 10 - y   we can substitute  10 - y  in for  x  in the second equation.

x²  -  y²   =   56

(10 - y)²  -  y²   =   56

(10 - y)(10 - y)  -  y²   =   56

100 - 20y + y²  -  y²   =   56

100 - 20y   =   56

-20y   =   -44

y   =   2.2

Using this value of  y  and the fact that   x  =  10 - y   we can find the value of  x

x   =   10 - y   =   10 - 2.2   =   7.8

So there is only one ordered pair of real numbers that satisfies the system of equations, and it is  (7.8, 2.2)

Let  f  be the age of the father and  s  be the age of the son.

The ratio of the age of the father to the age of the son 2 years ago was  10:1

The ratio of   f - 2   to   s - 2   =  10:1

f - 2 : s - 2   =   10:1

(f - 2) / (s - 2)  =  10/1

(f - 2) / (s - 2)  =  10

f - 2   =   10(s - 2)

f - 2   =   10s - 20

f   =   10s - 18

In 5 years, the age of the father will be  4  times the age of the son.

f + 5   =   4(s + 5)

f + 5   =   4s + 20

f   =   4s + 15

Now since   f  =  10s -18   and   f  =  4s + 15   we can say...

10s - 18  =  4s + 15

10s - 4s  =  15 + 18

6s  =  33

s  =  5.5

Now we can find the value of  f  using this value of  s

f   =   4s + 15   =   4(5.5) + 15   =   37

the difference in the age of the father and son   =   f - s   =   37 - 5.5   =   31.5

Lia ate  2/3  of the pizza which means she left  1/3 .

So her brother received  1/3  of  6/8  of a whole pizza.

That is,

the amount her brother received  =  1/3 * 6/8  of a whole pizza

\(\dfrac13\times\dfrac68\ =\ \dfrac{1\times6}{3\times8}\ =\ \dfrac{6}{24 }\ =\ \dfrac{1}{4}\)

So...

her brother received  1/4  of a whole pizza

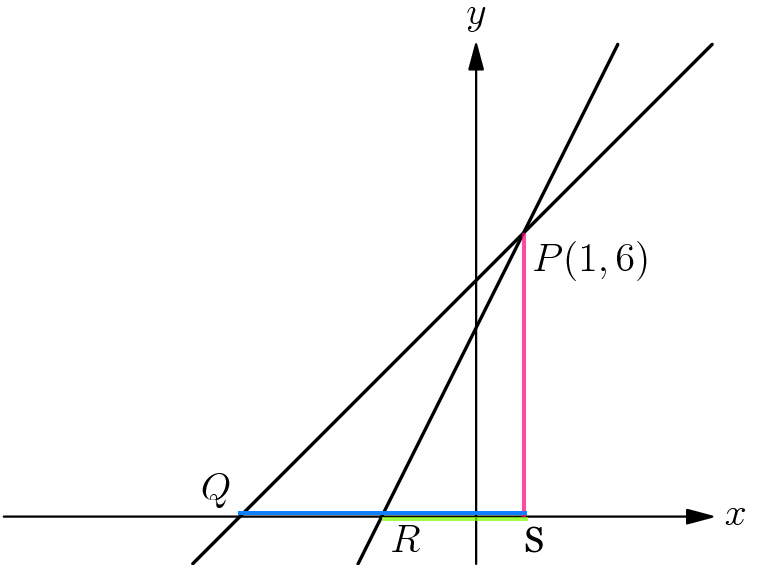
Let's draw a line straight down from  P  to the  x-axis  and call that point of intersection  S.

Now notice that the area of △PQR is equal to the area of △PQS minus the area of △PRS

Now since  P  is  6  units above the x-axis,

PS  =  6

From the picture we can see that PR has a steeper slope than PQ,

and so we can say the slope of PQ is  1  and the slope of PR is 3

Since  PQ  has a slope of  1,

rise / run  =  1

PS / QS  =  1

6 / QS  =  1

6  =  QS

QS  =  6

Since PR  has a slope of  3 ,

rise / run  =  3

PS / RS  =  3

6 / RS  =  3

6  =  3 * RS

2  =  RS

RS  =  2

Now we can find the area of  △PQS and the area of △PRS

area of △PQS   =   (1/2) * base * height   =   (1/2) * QS * PS   =   (1/2) * 6 * 6   =   18

area of △PRS   =   (1/2) * base * height   =   (1/2) * RS * PS   =   (1/2) * 2 * 6   =   6

And so...

area of △PQR   =   area of △PQS  -  area of △PRS   =   18 - 6   =   12

(Note... all areas are in square units)

Alternatively...we can do

area of  △PQR   =   (1/2) * base * height   =   (1/2) * QR * PS   =   (1/2) * 4 * 6   =   12

area of sector / area of circle  =  100 / 360

Let  r  be the radius of the circle   so   the area of the circle  =  π r²

Substitute  250π  in for the area of the sector and substitute  π r²  in for the area of the circle.

250π  /  (π r²)   =   100 / 360

                                               Cancel out the  π's  in the first fraction

250 / r²   =   100 / 360

                                               Flip both sides of the equation

r² / 250   =   360 / 100

                                               Multiply both sides of the equation by  250

r²   =   360 / 100 * 250

                                               Simplify the right side of the equation.

r²   =   900

                                               Take the positive square root of both sides.

r   =   30