CPhill

y=1/2x-2 and 4x-7y=15

Let's multiply the first equation by 2 to clear the fraction....this gives....

2y = x - 4              add 4 to both sides.......this gives........x = 2y + 4

Now, in the other equation, substitute for x

4(2y + 4) -7y = 15   

8y + 16 - 7y = 15

y + 16 = 15              Subtract 16 from both sides

y = -1       Now, use   x = 2y + 4 to find x

x = 2(-1) + 4   = -2 + 4 = 2

So...our solutions are   x = 2 and y = -1

You should check that these solutions "work" in both equations.

Just divide the numerator by the denominator.

simplify z-8/z -5z-38/11z

I'm going to assume that you either mean this:  z-8/z -5z-(38/11)z 

or this:   z- 8/z -5z-38/(11z)

If it's the first, we have  [z - 5z - (38/11)z)] - 8/z  = (-82/11)z - 8/z =

-[(82z^2 + 88] / (11z)]

If it's the second, we have (z - 5z) - [(38/(11z) + 8/z)]    = (-4z)  -[(38/(11z) + (88/(11z)] = -[44z^2 + (126)] / (11z)]

Let's write

y = 8x^3 - 6       Let's get x by itself   ....  add 6 to both sides

y + 6 = 8x^3      Divide by 8 on both sides

(y + 6) / 8   =   x ^3           Take the cube root of both sides.....

[(y + 6)/ 8]^(1/3)  = x        Now "swap" x and y

[(x + 6)/ 8]^(1/3)  = y        And, for y, write f ^-1(x) and there's the inverse

We can use an informal way to check that this is the inverse - it isn't foolproof, but it will work in most cases.....

Note that the inverse should "reverse" the x and y coordinates on a graph. So, in the original problem, let x = 1 and y will = 2. Then, in the inverse, let x =2, and we should get y =1...and we do!!   So, we're pretty sure it's correct.......

Here's the way  to do it...

To figure your share, it's just...

[(square footage you use)/ (total square footage)]  x  rent

And your roommate's share is just

[(square footage he/she uses)/ (total square footage)]  x  rent

I don't know much about this, but the way I understand it is that the infimum of a set of numbers is the largest number that is less than or equal to all the numbers in the set.
The supremum of a set of numbers is the smallest number that is greater than or equal to all the numbers in the set. 

Also, as I understand it, the infimum of a set doesn't actually have to belong to the set itself. Based on this, -2 should be your answer, because it's the largest number that is less than or equal to all the members of (-2, 3]. Notice that it doesn't belong to the set itself.

If someone on the forum knows more about this, I'll stand corrected......

When we divide, the 3t^2 +7t - 6 terms "cancel" with each other, so we're left with

(3t^2 - 11t + 6) / (9t^2 - 12t + 4)      Factoring, we have

[(3t - 2)(t - 3)] / [(3t -2)(3t - 2)]     And we're left with

(t - 3) / (3t - 2)

We can write

(-2 - √x)  (-2 - √x)

We can factor a "-1" out of both expressions

(-1) (2 + √x) * (-1)(2 + √x)   =      (-1)(-1)(2 + √x)(2 + √x) = (2 + √x)(2 + √x)

So, multiply the 2's together to get 4

And multiplying 2 times √x  and 2 times √x and adding them together gives 4√x

And √x *√x  = x

So putting all this together gives us

4 + 4√x + x

The compound interest formula is given by:

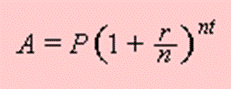
Where

P = principal amount (the initial amount you borrow or deposit)

r  = annual rate of interest (as a decimal)

t  = number of years the amount is deposited or borrowed for.

A = amount of money accumulated after n years, including interest.

n  =  number of times the interest is compounded per year

 To solve for t......

First divide both sides by P

Now, take the log of both sides....this will give us

log (A/P) = log (1 + r/n)^nt

And by a  property of logs, we can bring the (nt) "out front," and we can write

log (A/P) = (nt)* log (1 + r/n)    ........ Now divide both sides by n  and log(1 + r/n)

So we have

[log (A/P)] / [n * log(1 + r/n] = t

And that's what "t" is

We need a picture of "A" or some other information - like two points that lie on "A."