In a certain pentagon, the interior angles are A B C D and E where A B C D E are integers strictly less than 180 ("Strictly less than 180" means they are "less than and not equal to" 180.)
If the median of the interior angles is 61 and there is only one mode,
then what are the degree measures of all five angles?
See the answer here: https://web2.0calc.com/questions/help_53845
![]()
the positive integers are arranged in the pattern illustrated below if this pattern continues indefinitely, what is the number immediately above 39863?
1 2 5 10 17 26
3 4 7 12 19 28
6 8 9 14 21 30
11 13 15 16 23 32
18 20 22 24 25 34
27 29 31 33 35 36
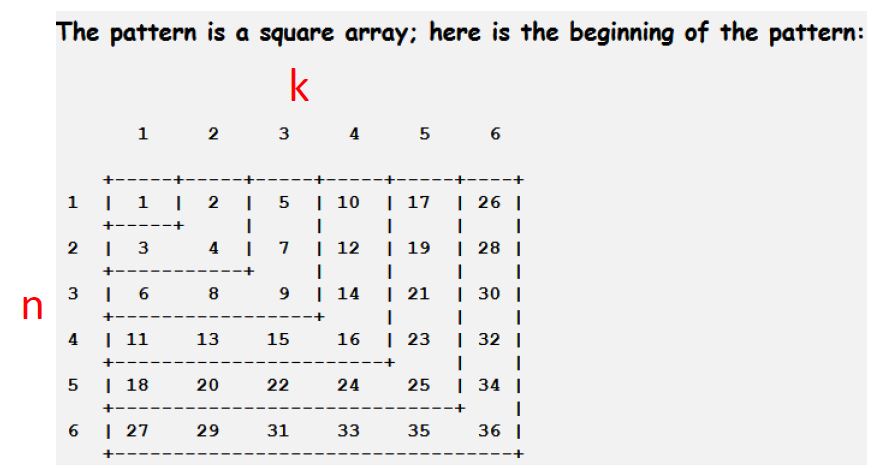
Let row = n
Let column = k
Formula:
\(\begin{array}{|rcll|} \hline T(n,k) &=& (k-1)^2+2n-1 \qquad & n\le k \\ T(n,k)&=&(n-1)^2+2k \qquad & n>k \\ \hline \end{array}\)
Source: http://oeis.org/search?q=a185725&sort=&language=english
1. \(\begin{array}{|rcll|} \hline \sqrt{39863} &=& 199.657\ldots \\ n_{min} &=& 199 \\ n_{max} &=& 200 \\ \hline \end{array}\)

\(\begin{array}{|rcll|} \hline T(200,k) &=& (200-1)^2+2k \qquad & n>k \\ 39863 &=& 199^2+2k \\ 2k &=& 39863 - 199^2 \\ 2k &=& 262 \\ \mathbf{k}& \mathbf{=}& \mathbf{131} \\ \hline \end{array} \)
The number immediately above:
\(\begin{array}{|rcll|} \hline T(199,131) &=& (199-1)^2+2\cdot 131 \qquad & n>k \\ T(199,131) &=& 198^2+2\cdot 131 \\ \mathbf{T(199,131)} & \mathbf{=}& \mathbf{39466} \\ \hline \end{array}\)
![]()