+15000 Hallo anonymous!
Um die Antwort auf deine Frage ist zu allen Zeiten immer wieder gerungen worden.
Eine Weltformel, oder eine Theorie von Allem (englisch theory of everything, ToE oder TOE) ist eine hypothetische Theorie gebildet aus theoretischer Physik und Mathematik, die alle bekannten physikalischen Phänomene erklären und verknüpfen soll.
In der Komödie Die Physiker von Friedrich Dürrenmatt wird die Weltformel von einem Physiker namens Johann Wilhelm Möbius gefunden. Allerdings versteckt er diese vor der Allgemeinheit, weil er eine Gefährdung der Menschheit befürchtet, wenn diese und seine anderen Arbeiten an die Öffentlichkeit gelangen.
In Darren Aronofskys Film Pi findet der Mathematiker Maximillian Cohen ebenfalls eine Art Weltformel, die von verschiedenen Parteien heiß begehrt ist; unter anderem weil man mit ihrer Hilfe die Zukunft vorhersagen könnte.
Ich glaube, es wäre es gut so, wenn diese "Weltformel" nie gefunden würde.
Gruß asinus :- )
+15000 Hallo anonynymous!
Der Elastizitätsmodul von Stahl ist
E = 210 kN/mm²
Bei ideal linear elastischem Werkstoffgesetz (Proportionalitätsbereich im Spannungs-Dehnungs-Diagramm) ergibt sich die Federkonstante c eines geraden Stabes aus seiner Querschnittsfläche A, seiner Länge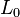 
und seinem Elastizitätsmodul E.
Mit den Ausdrücken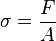 
für die Spannung und 
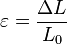für die Dehnung erhält man aus obiger Gleichung das Hookesche Gesetz für den einachsigen Spannungszustand
und daraus den E-Modul
1. A = d²*pi/4 = 0,1²mm²*pi/4
Der Querschnitt
A = (7,854 / 10³)mm²
2. σ = F/A = (5kg * 9,81m/s²)/(7,854mm²/10³)
Die Spannung
σ = 6245,225 N/mm²
3. ε = σ/E = (6245,225 N/mm²)/(210*10³ N/mm²)
Die Dehnung
ε = 0,02974
4. ΔL = L(0) * ε = 1 500mm * 0,02974
Die Längenänderung (theoretisch, weil der Draht vorher reißt)
(ΔL = 44,6mm )
5. Baustahl St37 hat eine Zugfestigkeit von σ(Br) = 37kp/mm² = 363N/mm²
F(Br) = σ(Br) * A = (363N/mm²)*(7,854/10³)mm²
Die notwendige Kraft zum Zerreißen des Drahtes aus St37 ist
Bei m = 2,851N / 9,81m/s² = 0,291kg angehängter Masse reißt der Draht.
Vielen Dank für Ihren Hinweis auf meinen Fehler Omi67! 
Gruß asinus :- )
+15000 Hello anonymous!
4.05-tan(x) = cos(x)*3.9 [ cosx = 1 / √(1 + tan²x)
4,05-tanx =3,9/√(1+tan²x)
√(1+tan²x) * (4,05-tanx) = 3,9 [ tanx = z
√(1+z²) * (4,05-z) = 3,9 [ 1. / (4,05 -z) 2. Quadrieren
1+z² = (3,9/(4,05-z))²
1+z² = 3,9²/(4,05²-8,1z +z²) [ * (4,05²-8,1z +z²) und gleich ausmultiplizieren
4,05²-8,1z +z² + 4,05²z² -8,1z³ + z^4 = 3,9²
z^4 - 8,1z³ +17,4025z² - 8,1z + 1,1925 = 0
http://equationsolver.intemodino.com/de/gleichungen-4-grades-loesen.html
x^4 - 8.1x^3 + 17.4025x^2 - 8.1x + 1.1925 = 0
Die Gleichung hat 2 reelle Lösungen und 2 komplexe Lösungen
x1 = 4.8392373 = z(1)
x2 = 2.6918853 = z(2)
x3 = 0.2844387+0.1031387i
x4 = 0.2844387-0.1031387i
z(1) = tan (x1) = 4,8392373
x1 = atan z(1) = 78,3245°
z(2) = tan (x2) = 2,6918853
x2 = atan z(2) = 69,6206°
Gruß asinus :- )
